Michaelis-Menten Kinetics
MCAT Biochemistry - Chapter 3 - Section 2.1 - Enzymes - Michaelis-Menten Kinetics
- Home
- »
- MCAT Masterclass
- »
- Biological and Biochemical Foundations of Living Systems
- »
- Biochemistry
- »
- Michaelis Menten Kinetics – MCAT Biochemistry
Sample MCAT Biochemistry Question
a) Increase substrate concentration
b) Decrease enzyme concentration
c) Add a non-competitive inhibitor
d) Increase enzyme concentration
D is correct. Increase enzyme concentration.
In terms of Michaelis-Menten kinetics, when the maximum speed of the reaction is achieved (Vmax), all of the enzymes in the reaction are saturated. In this way, adding more substrate will not increase the speed of the reaction (choice A is incorrect). Typically, the only way to increase the Vmax is to increase the enzyme concentration so that there are more active sites to interact with substrate molecules. Choice B is incorrect as it is the opposite of the correct answer. Choice C is incorrect, as adding the concentration of non-competitive inhibitor would result in a decrease in Vmax.
Enzymes
In order to understand Michaelis-Menten kinetics, it is important to review the basic function of enzymes. Enzymes are biological catalysts that are generally made of proteins, but sometimes they are made of RNA molecules as well. As catalysts, there are several features of enzymes that are important to understand. First, enzymes increase the rate of a reaction by decreasing the activation energy. Enzymes accomplish this by stabilizing the transition state. Second, there is no net consumption or production of enzymes during a reaction. Therefore, it is said that enzymes are recycled during a chemical reaction. Lastly, enzymes are reaction-specific. For example, first step of glycolysis is catalyzed by the enzyme hexokinase, which converts glucose into glucose-6-phosphate. Hexokinase, however, is not able to catalyze any of the other steps in glycolysis. Thus, hexokinase is specific to this reaction.
Michaelis Menten Kinetics
The Michaelis Menten kinetics model describes the general catalysis of enzymatic reactions. Figure 1 shows an equation that represents the basic concept of this model. The enzyme (E) binds to the substrate (S) to form the enzyme-substrate (ES) complex. The ES-complex can then react to form the enzyme and the product.
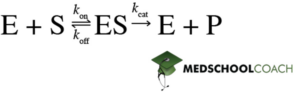
Other essential features of this equation include the variables k1, k2, and k3. Recall from General Chemistry, that lowercase k stands for the rate constant, which is a description of the speed of a reaction. In this model, k2 can also be understood as kon, k1 as koff, and k3 as kcat. In this way, kon (k2) is how fast the enzyme binds to the substrate to form the enzyme-substrate complex (ES). Likewise, koff (k1) is how fast the enzyme-substrate complex (ES) dissociates to form the free enzyme (E) and substrate (S). Finally, kcat (k3) refers to how fast the enzyme-substrate complex (ES) forms that enzyme (E) and product (P). Also, it is important to note that the first step in this equation is reversible, meaning it can go in the forward or reverse direction. However, the second step can only go in the forward direction and is irreversible.
Michaelis Menten Equation
From the Michaelis-Menten model, scientists derived the following equation:
V0 = (Vmax x [S]) / (KM + [S])
This equation is describing V0 or the reaction velocity. The reaction velocity (V0) is how fast products are being formed. Vmax describes the maximum reaction velocity, and [S] is the substrate concentration. The variable Km is the Michaelis constant. It is equal to the substrate concentration when the reaction velocity (V) is equal to half the maximum reaction velocity, or half Vmax. The KM value is dependent on several factors, like the specific identity of the enzyme and substrate, the temperature of the reaction, as well as the pH. Also, in equation form KM = koff + kcat / kon. Overall, the Michaelis-Menten equation describes how fast a reaction proceeds at specific substrate concentrations.
Assumptions of Michaelis Menten Kinetics
For the MCAT exam, it is important to understand certain key assumptions that were made in deriving the Michaelis-Menten equation. In this way, it is possible to discern when the equation can be used and when it cannot be used.
The first assumption is that this equation is only used to describe the initial reaction velocity. The subscript “0” accompanying the variable V0 represents this assumption. One of the consequences of this assumption is that the substrate concentration is much greater than the product concentration. In the initial stage of the reaction, not much product is formed, so this assumption makes sense.
Another assumption of the Michaelis-Menten model is that the enzyme-substrate complex concentration [ES] is constant. This concept is known as steady-state approximation. Figure 1 shows that the enzyme-substrate (ES) complex can either be consumed or produced. Production of the ES-complex occurs when the enzyme binds to the substrate. Consumption of the ES-complex can occur in two ways. One, it can dissociate to reform the free enzyme and substrate, or two, it can react to form the enzyme and the product. Steady-state approximation states that the rate of ES-complex formation is equal to its rate of consumption.
The third assumption of the Michaelis-Menten model is that the substrate concentration [S] is approximately equal to the total substrate concentration. Technically, the total substrate concentration in the solution is equal to the concentration of substrate [S] plus the concentration of enzyme-substrate complex [ES]. However, assuming that [S]>>>[E], it can be assumed that the substrate concentration [S] is approximately equal to the total substrate concentration. This concept is known as free ligand approximation.
The fourth and final assumption of the Michaelis-Menten model is that the rate constants for the first step of the reaction, kON and kOFF, are much greater than the rate constant for the second step of the reaction, kCAT. In terms of the equation for KM, where KM = (kOFF + kCAT) / kON, if kOFF is much greater than kCAT, then KM is simply kOFF / kON. Also, the rate constant for dissociation (kOFF) over the rate constant for association (kON) is equal to Kd, the dissociation constant for the equilibrium of the first step of the reaction. Also, recall that Kd is a measure of the affinity of the enzyme for the substrate. That is, the higher the Kd value, the smaller or lower the affinity of the enzyme for its substrate. In other words, Kd is inversely related to the affinity of the enzyme for the substrate. In this way, since the value of Kd and KM are both equal to kOFF/kON, then Kd and KM are mostly the same. Thus, KM is also inversely related to the affinity of the enzyme for the substrate under this final assumption.
Catalytic Efficiency
Catalytic efficiency is the efficiency of an enzyme for producing products, and it depends on two factors: kCAT and KM (catalytic efficiency = kCAT / KM). Recall that kCAT is how fast catalysis occurs, or in other words, how fast the enzyme-substrate complex (ES) can form enzyme (E) and product (P). The higher the value of kCAT is, the more efficient the enzyme. Also, catalytic efficiency is inversely related to KM. In order to have a very efficient enzyme, it should have a high affinity for its substrate and be able to bind easily. As we noted previously, Km is inversely related to affinity. Having a high affinity, or a more efficient enzyme, indicates a low KM value. A smaller KM value contributes to increasing an enzyme’s catalytic efficiency.
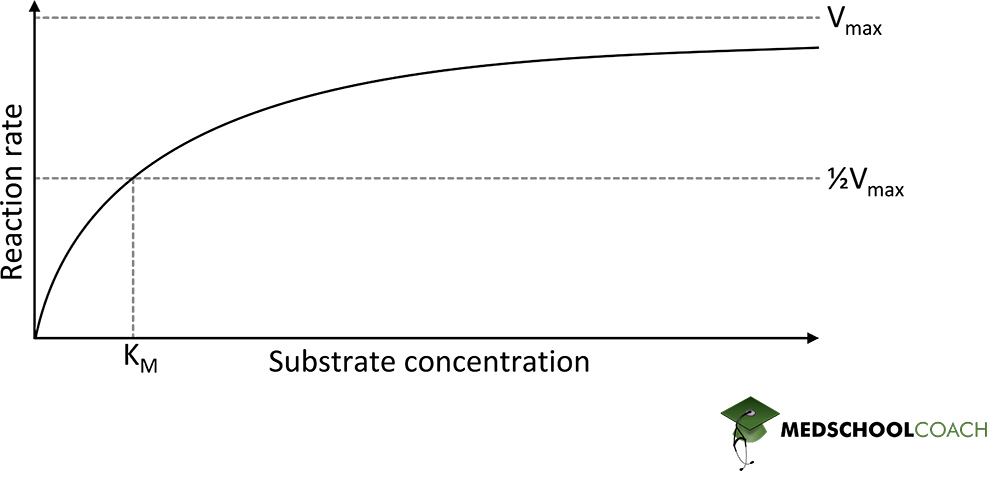
Michaelis-Menten Saturation Curve
The Michaelis Menten saturation curve is a pictorial representation of the Michaelis Menten equation. In the curve, as the substrate concentration increases, the reaction velocity also increases. However, at some point, the velocity reaches a maximum value, which is Vmax, or the maximum reaction velocity. The maximum reaction velocity (Vmax) occurs when an enzyme is saturated by a substrate. Also, recall that KM is ½Vmax, which are both variables that can be derived from the Michaelis Menten saturation curve. Lastly, it is important to note that the Michaelis Menten saturation curve is hyperbolic. For the MCAT, you may see the data from a Michaelis Menten saturation curve presented in a different format called the Lineweaver Burk plot. In addition, the exam also commonly tests the effects of different types of enzyme inhibitors on the Michael Menten saturation curve.
Explore More MCAT Masterclass Chapters
Take a closer look at our entire MCAT Masterclass or explore our Biochemistry lessons below.

One-on-One Tutoring
Are you ready to take your MCAT performance to a whole new level? Work with our 99th-percentile MCAT tutors to boost your score by 12 points or more!
See if MCAT Tutoring can help me
Talk to our enrollment team about MCAT Tutoring

MCAT Go Audio Course
Engaging audio learning to take your MCAT learning on the go, any time, any where. You'll be on the way to a higher MCAT score no matter where you are. Listen to over 200+ lessons.
MCAT Practice Exams
Practice makes perfect! Our mock exams coupled with thorough explanations and in-depth analytics help students understand exactly where they stand.
MCAT Prep App
Access hundreds of MCAT videos to help you study and raise your exam score. Augment your learning with expert-created flashcards and a question banks.