Zwitterions and Isoelectric Point
MCAT Biochemistry Chapter 1 - Section 1.3 - Amino Acids - Zwitterions and Isoelectric Point
- Home
- »
- MCAT Masterclass
- »
- Biological and Biochemical Foundations of Living Systems
- »
- Biochemistry
- »
- Amino Acids
- »
- Zwitterions and Isoelectric Point – MCAT Biochemistry
Sample MCAT Question - Zwitterions and Isoelectric Point
Which of the following are characteristics of zwitterions?
I. They contain positive charges
II. They contain negative charges
III. They have a net charge of 0
a) I only
b) II only
c) I and II only
d) I, II, and III
D is correct. I, II, and II.
All three of the choices are characteristics of zwitterions. Also known as dipolar ions, these molecules have both positive and negative charges, but a net charge of zero.
Get 1-on-1 MCAT Tutoring From a Specialist
With MCAT tutoring from MedSchoolCoach, we are committed to help you prepare, excel, and optimize your ideal score on the MCAT exam.
For each student we work with, we learn about their learning style, content knowledge, and goals. We match them with the most suitable tutor and conduct online sessions that make them feel as if they are in the classroom. Each session is recorded, plus with access to whiteboard notes. We focus on high-yield topics if you’re pressed for time. If you have more time or high-score goals, we meticulously cover the entire MCAT syllabus.
Zwitterions and Isoelectric Point
In this post, we’ll define the concept of zwitterions and then discuss the conditions under which amino acids exist as zwitterions. This, as we’ll find out, depends on the protonation state of the amino acid, which in turns depends on the pKa of its functional groups as well as the pH of the surrounding solution. This post will also cover the concept of the isoelectric point (pI), the pH at which all of the molecules of a certain amino acid are in their zwitterionic form, and will show you how to calculate pI for different amino acids.
What Are Zwitterions?
Zwitterions, sometimes called dipolar ions are molecules with an equal number of positive and negative charges. Therefore, though the molecules themselves are ions, their net charge is zero.
Amino Acids as Zwitterions
Recall the basic structure of amino acids — every amino acid contains both a carboxylic acid group (COOH) and an amino group (NH2) attached to the α-carbon, as shown in Figure 1 below.
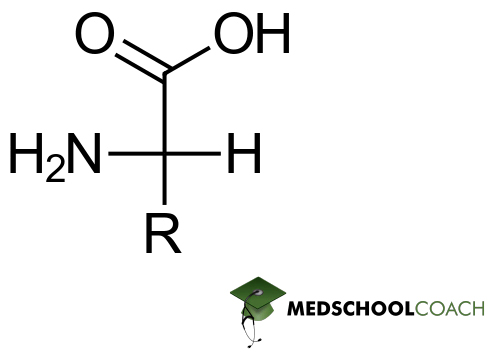
In this figure, the α-amino group is in a deprotonated state while the α-carboxyl group is in a protonated state. Thus, while this particular amino acid has a net charge of zero, it is not in its zwitterionic form because it contains no charges whatsoever — for a molecule to count as a zwitterion, it has to actually contain positive and negative charges, but these charges must also add up to zero.
So when are amino acids in their zwitterionic form? Well, it depends on the type of amino acid. Polar and non-polar amino acids don’t have an ionizable side chain, which means that their α-amino and α-carboxyl groups are the only groups capable of being protonated and deprotonated. These amino acids are therefore in their zwitterionic form when their α-amino group is protonated and has a +1 charge and when their α-carboxyl group is deprotonated and has a -1 charge. In this particular protonation state, the amino acid is charged but the charges cancel out, which means that it meets the criteria for being a zwitterion.
pH, pKa, and Isoelectric Point
At this point, you may be wondering what’s responsible for the protonation states of amino acids — how do amino acid functional groups go from being protonated to deprotonated and vice-versa?
Well, it turns out that the protonation state of a given functional group depends on two factors: its pKa and the pH the surrounding solution. To refresh your memory, pH is a measure of how acidic a solution is. Mathematically, it is defined as the negative logarithm of the concentration of H+ ions in a given solution. This means that the lower the pH of a solution, the more hydrogen ions it has and the more acidic it is. pKa, on the other hand, is a measure of a functional group‘s acidity — its tendency to give up its protons. More formally, the pKa of a functional group is the pH at which that functional group is 50% protonated and 50% deprotonated. So when pH equals the pKa of a certain functional group on a molecule, half of those molecules will have the protonated version of that functional group while the other half will have the deprotonated version.
Now, with this in mind, let’s consider a polar or non-polar amino acid, i.e. one that does not have an ionizable side chain. As we’ve already covered, these amino acids have two ionizable function groups: an α-amino functional group and a α-carboxyl functional group. The latter, being acidic, has a pKa of around 2, while the former, being basic, has a pKa of around 9. This means that when the pH of solution is 2, half the amino acid molecules will be in a cationic form, where the α-carboxyl group is protonated and therefore neutral, while the other half will be in a zwitterionic form, where the α-carboxyl group is deprotonated and therefore negatively charged. (An amino acid in its fully protonated, cationic form and in its zwitterionic form is shown in Figure 2, on the left and in the center respectively.)
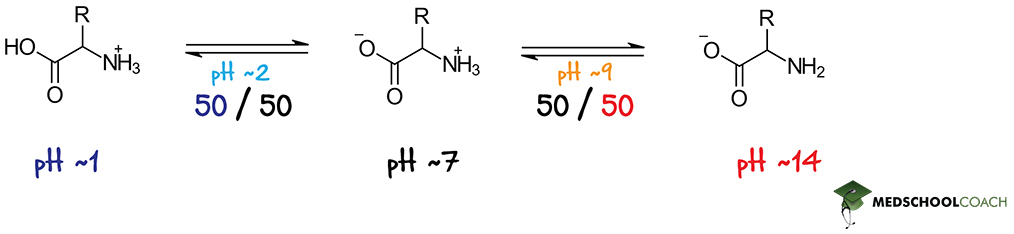
Now let’s consider what happens when the pH starts to rise. When pH rises, the solution becomes less acidic and therefore contains fewer H+ ions. This means that the molecules in solution, like our amino acid, will be more inclined to lose their protons to the surrounding solution. We can therefore predict that as pH begins to exceed 2 (the pKa of the carboxyl functional group), more and more amino acids will assume their zwitterionic form, where the α-carboxyl group is deprotonated. Eventually, there will come a point where all the amino acids in solution will exist as zwitterions. This point is known as the isoelectric point, which is formally defined as the pH at which all of molecules of a certain type are in their zwitterionic form.
Eventually, however, as pH approaches the pKa of the α-amino functional group (which, again, is around 9), that functional group will also start to lose its protons. At this point, the surrounding solution has so few H+ ions that even basic groups, like our amino group, can’t hold on to their protons. When pH equals 9, only half of the amino acids will exist as zwitterions — the other half will have assumed an anionic form, where even the α-amino group is deprotonated. Eventually, when pH rises high enough, all the amino acids in solution will exist in their fully deprotonated, anionic form. (An amino acid in this form is shown on the right in Figure 2.)
Basic and Acidic Amino Acids as Zwitterions
Thus far, we’ve discussed amino acids as if they only have two ionizable functional groups: the α-carboxyl group and the α-amino group. This is true for polar and nonpolar amino acids, which don’t have ionizable side chains. But some amino acids — those amino acids classified as either basic or acidic — do have ionizable side chains. Determining when these exist as zwitterions is a bit more complicated since now we’re dealing with three different ionizable functional groups (the α-carboxyl, α-amino, and side chain groups) with three different pKa values rather than just two.
For the sake of example, let’s consider the basic amino acid lysine. Its α-carboxyl group has a pKa value of about 2 and its α-amino group has a pKa of about 9, just like the other amino acids. But as you can see in Figure 3, it also has a ionizable side chain with a pKa of about 10.7. With this in mind, let’s walk through the various protonation states of lysine.
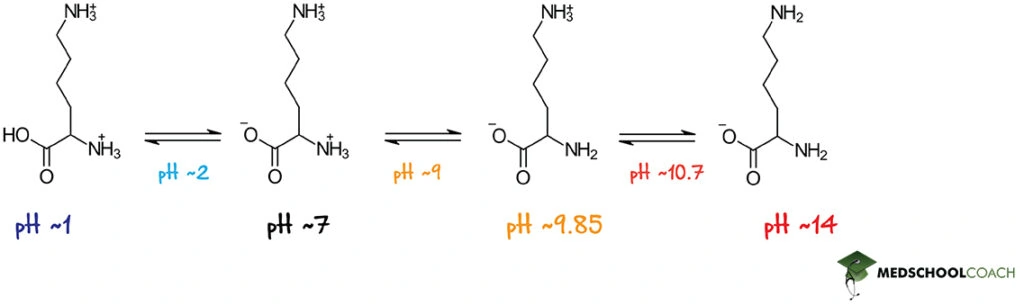
Let’s begin by considering a solution with a pH of 2, which is equal to the pKa of the α-carboxyl group. At this pH, half the lysine molecules in solution will have a protonated α-carboxyl group and a net charge of +2, while the other half will have a deprotonated α-carboxyl group and therefore a net charge of +1. (These two protonation states are shown on the left in Figure 3.) As pH increases, there will eventually come a point where all of the lysines in solution will be deprotonated at their α-carboxyl functional group and will therefore have a +1 net charge. According to Figure 3, this will occur somewhere between pHs 2 and 9.
As pH nears 9, however, α-amino functional groups will also start to become deprotonated. Once this occurs, there are only two charges left on the lysine molecule: a -1 charge on the α-carboxyl group and a +1 charge on the side chain. These charges sum to 0, which means that this particular protonation state (second from the right in Figure 3) is lysine’s zwitterionic form. At a pH of 9, half of all lysine molecules will exist in this form, while the other half will retain a protonated α-amino group and a net charge of +1. Eventually, however, as pH rises above 9, this latter species will cease to exist and all the lysine molecules will exist as zwitterions. The pH at which this occurs is lysine’s isoelectric point.
Once pH rises above the isoelectric point, however, lysine’s most basic functional group, its side chain group, will also start to lose its protons. At a pH of 10.7, equal to the pKa of the side chain, half of all lysine molecules will be fully deprotonated and have a net charge of -1, while the other half will remain as neutral zwitterions. As pH continues to rise, however, fewer and fewer zwitterions will remain, until eventually all the lysine molecules in solution will be in their fully deprotonated, anionic form. (This form of lysine is shown rightmost in Figure 3.)
Calculating Isoelectric Point (pI)
We’ve discussed isoelectric point (pI) in rather vague terms thus far, merely saying that it is the pH at which all of the molecules of a certain amino acid exist as zwitterions. You may now be wondering if there is a way to determine this pH value exactly. The answer, happily for science, is yes. Figure 4 shows an equation you can use to calculate the pI. You should memorize this equation for test day.
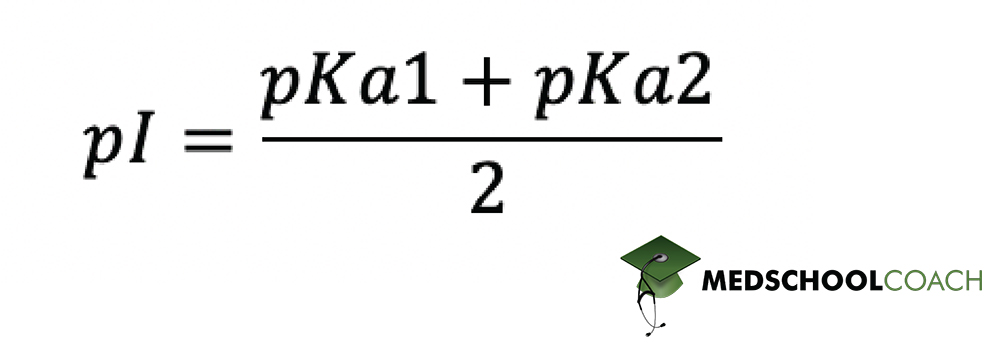
In the Figure 4 equation, pKa1 and pKa2 stand for the pKa’s of the relevant functional groups on the molecule in question. In the case of polar and nonpolar amino acids, which don’t have an ionizable side chain group, pKa1 and pKa2 stand for the pKa’s of the α-cabroxylic acid group and the α-amino group. Since these are 2 and 9 respectively, we can calculate pI as shown in Figure 5. As you can see, pI for polar and non-polar amino acids comes out to about 5.5.
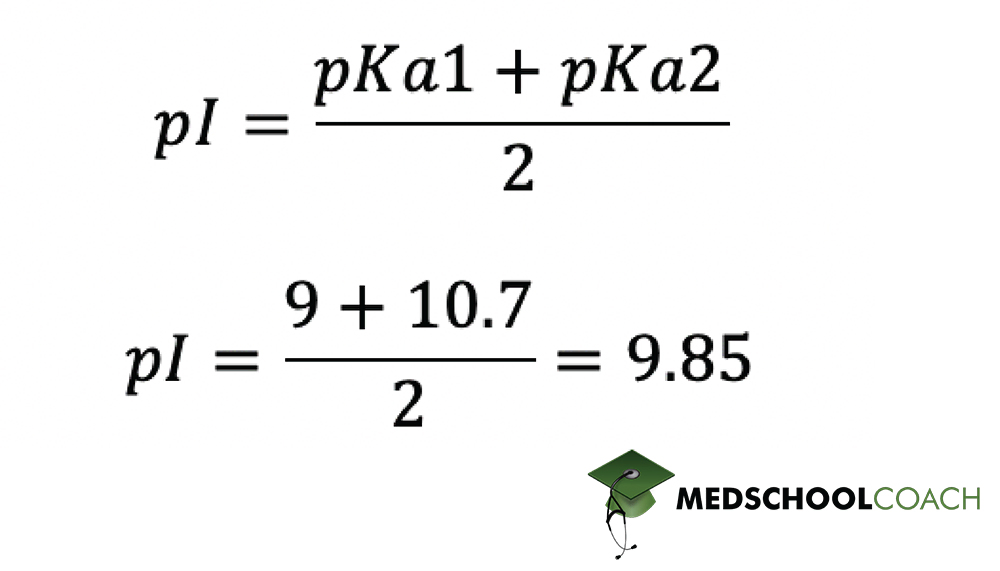
The same equation can also be applied to calculating pI for acidic and basic amino acids — those which do have an ionizable side chain. However, you need to be careful about selecting the correct pKa values to plug into the equation. Take lysine, for instance, the basic amino acid from the previous example. As we discovered previously, the isoelectric point for lysine lies somewhere between 9 and 10.7, the pka’s of lysine’s α-amino group and basic side chain respectively. These are therefore the values we plug into the equation, as shown in Figure 6. Based on the equation, pI for lysine is around 9.85.
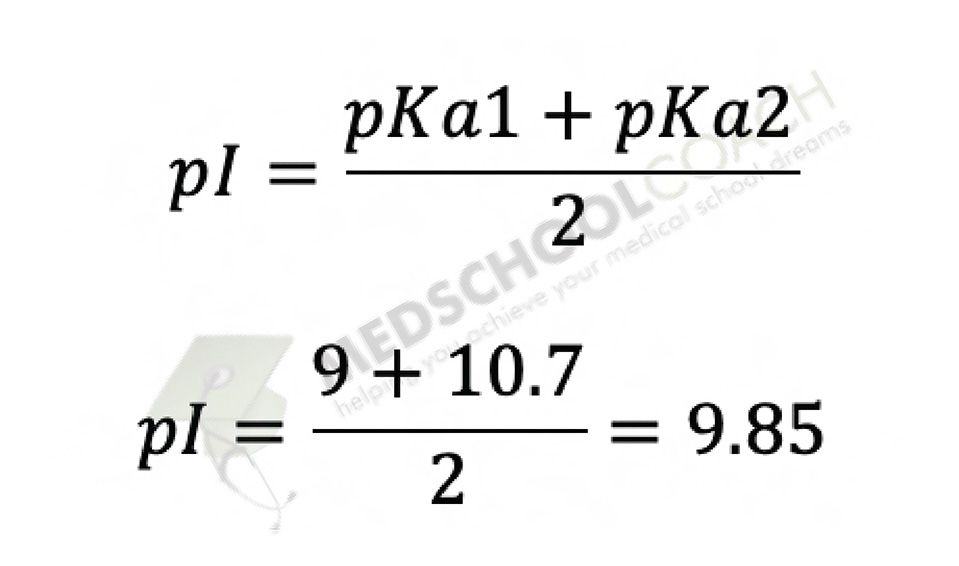
When you’re dealing with acidic and basic amino acids, it might be tempting to simply plug in the values of the α-carboxyl and the α-amino group, as we did for the polar/nonpolar amino acids. However, this would be incorrect. To see why, look back at Figure 3. At a pH of 9 (the pKa of the α-amino group), half the lysines in solution would have a net charge of +1, while the other half would be zwitterions and have a net charge of 0. At a pH of 2, however (the pKa of the α-carboxyl group), half the lysines would have a net charge of +2, half would have a net charge of +1, and exactly none would exist as zwitterions with a net charge of 0. The isoelectric point of lysine cannot therefore lie between pHs 2 and 9. An consequently, these are not the values we plug into the equation. Instead, the isoelectric point must lie somewhere above pH 9, so we therefore choose the two higher pKa values (9 and 10.7) to plug into the equation.
The overall point here is that when you’re dealing with acidic and basic amino acids with an ionizable side chain, you have to understand the various protonation states — and which one corresponds to the amino acid’s zwitterionic form — before you dive in and use the equation.
Predicting the Net Charge of Peptides
This post was all about how to determine the protonation state of an amino acid given the pKa of its ionizable groups and the pH of the surrounding solution. We then used this information to determine the amino acid’s isoelectric point, as shown above. We can also, it turns out, conduct the same sort of analysis with peptides and polypeptides. Since these are composed of amino acids, they also have a specific isoelectric point, a pH at which they carry no net charge. Determining the protonation state and net charge of peptides is the subject of another MCAT content post.
Explore More MCAT Masterclass Chapters
Take a closer look at our entire MCAT Masterclass or explore our Biochemistry lessons below.

One-on-One Tutoring
Are you ready to take your MCAT performance to a whole new level? Work with our 99th-percentile MCAT tutors to boost your score by 12 points or more!
See if MCAT Tutoring can help me
Talk to our enrollment team about MCAT Tutoring

MCAT Go Audio Course
Engaging audio learning to take your MCAT learning on the go, any time, any where. You'll be on the way to a higher MCAT score no matter where you are. Listen to over 200+ lessons.
MCAT Practice Exams
Practice makes perfect! Our mock exams coupled with thorough explanations and in-depth analytics help students understand exactly where they stand.
MCAT Prep App
Access hundreds of MCAT videos to help you study and raise your exam score. Augment your learning with expert-created flashcards and a question banks.